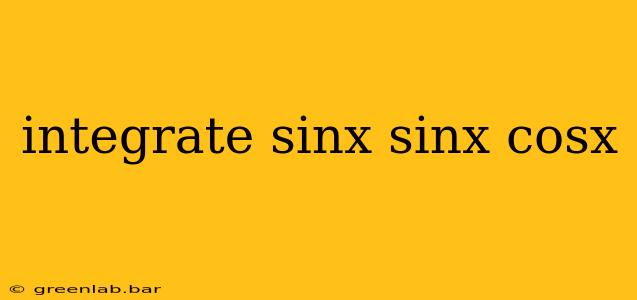Integrating trigonometric functions can often seem daunting, but with a systematic approach, even complex expressions become manageable. This guide will walk you through the process of integrating sin x sin x cos x, providing a clear, step-by-step solution and offering insights into the techniques used. The integral we're tackling is:
∫ sin²x cos x dx
Understanding the Problem
Before diving into the solution, it's crucial to understand what we're aiming to achieve. We're looking for a function whose derivative is sin²x cos x. This involves applying techniques of integration, specifically substitution.
Solving the Integral using Substitution
The most effective method for this integral is u-substitution. Let's choose our substitution:
Let u = sin x
Now we need to find the derivative of u with respect to x:
du/dx = cos x
Rearranging this gives us:
du = cos x dx
Notice that 'cos x dx' appears in our original integral! This makes our substitution incredibly useful.
Replacing sin x with u and cos x dx with du in our original integral, we get:
∫ u² du
Integrating the Simplified Expression
This simplified integral is much easier to solve. We apply the power rule of integration:
∫ uⁿ du = (uⁿ⁺¹)/(n+1) + C (where C is the constant of integration)
Applying the power rule with n=2:
∫ u² du = (u³)/3 + C
Substituting Back to x
Remember, our solution is currently in terms of 'u'. To express the final answer in terms of the original variable 'x', we need to substitute back using our initial substitution: u = sin x
Therefore, our final solution is:
(sin³x)/3 + C
Verification Through Differentiation
To verify our solution, we can differentiate the result and see if it matches the original integrand. Let's differentiate (sin³x)/3 + C:
d/dx [(sin³x)/3 + C] = (3sin²x * cos x)/3 = sin²x cos x
This matches our original integrand, confirming the accuracy of our integration.
Conclusion: A Step-by-Step Approach to Integration
This comprehensive guide demonstrates how to successfully integrate sin x sin x cos x (or sin²x cos x) using u-substitution. By strategically choosing a substitution, simplifying the expression, applying the power rule, and finally substituting back to the original variable, we arrive at a precise and verifiable solution: (sin³x)/3 + C. Remember, practice is key to mastering integration techniques. Working through similar problems will reinforce your understanding and build your confidence in tackling more complex integrals.