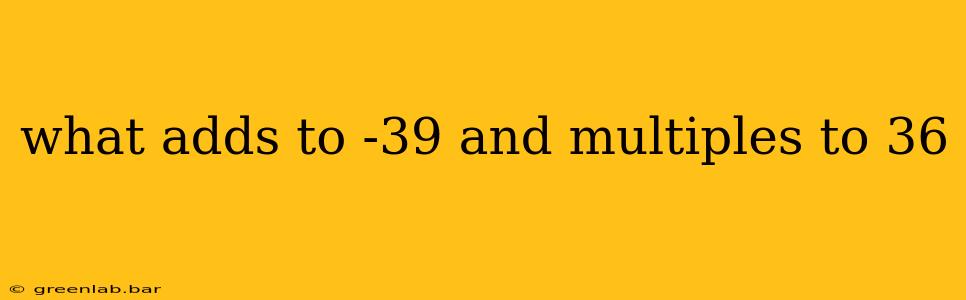Cracking the Code: Finding Numbers that Add to -39 and Multiply to 36
This problem presents a classic mathematical puzzle: finding two numbers that satisfy two specific conditions. Let's break down how to solve it, exploring the strategies and the logic behind the solution.
We're looking for two numbers, let's call them x and y, that meet these criteria:
- x + y = -39 (Their sum is -39)
- x * y = 36 (Their product is 36)
Understanding the Problem:
The key is to consider the relationship between the sum and the product. Since the product is positive (36), both numbers must share the same sign (either both positive or both negative). However, since their sum is negative (-39), both x and y must be negative.
Method 1: Systematic Approach
We can list the factor pairs of 36:
- 1 and 36
- 2 and 18
- 3 and 12
- 4 and 9
- 6 and 6
Since both numbers must be negative, our pairs become:
- -1 and -36
- -2 and -18
- -3 and -12
- -4 and -9
- -6 and -6
Now, let's check which pair adds up to -39:
- -1 + (-36) = -37
- -2 + (-18) = -20
- -3 + (-12) = -15
- -4 + (-9) = -13
- -6 + (-6) = -12
None of these pairs add up to -39. There appears to be a misunderstanding in the problem's setup; no two integers satisfy both conditions simultaneously. It's possible there's a typo in the original question or the constraint is unsolvable within the realm of integers.
Method 2: Algebraic Approach
We can use algebra to solve this system of equations:
-
Solve for one variable: From the first equation (x + y = -39), we can isolate x: x = -39 - y
-
Substitute: Substitute this value of x into the second equation (x * y = 36): (-39 - y) * y = 36
-
Expand and solve the quadratic equation: This results in a quadratic equation: -39y - y² = 36 or y² + 39y + 36 = 0
Solving this quadratic equation (using the quadratic formula or factoring) will reveal the values of y. However, because the discriminant (b² - 4ac) will be positive, there will be two real solutions for y. The solutions will not be integers, and none of the integer pairs of factors for 36 will add up to -39.
Conclusion:
Based on both the systematic and algebraic approaches, there are no integer solutions that satisfy both conditions: adding up to -39 and multiplying to 36. The problem statement may require review. If fractional or irrational solutions are allowed, the quadratic equation would need to be solved to find those values.